Creando coches para el juego

En esta entrada se va a hablar acerca del componente de dinámica de vehículos que incorpora Bullet Physics, el motor de físicas que se está usando en este proyecto. Se explicará como inicializar el vehículo y los elementos mas relevantes de éste módulo de Bullet. Por último, mostraremos un pequeño ejemplo que servirá para ejemplificar lo hablado en esta entrada.
Pero para empezar, vamos a introducir brevemente los principios físicos que permiten el movimiento de un coche.
Un poco de teoría
A grandes rasgos, el movimiento de un coche radica en un conjunto de fuerzas que se aplican sobre las ruedas y el chasis del vehículo. En la dirección del movimiento del coche se aplica una fuerza longitudinal, compuesta por la fuerza que aplican las ruedas, la fuerza de frenado, la resistencia que oponen los neumáticos y la resistencia del aire. Por otro lado, en giros existen fuerzas laterales causadas por la fricción lateral de las ruedas, además del momento angular del coche y el esfuerzo de torsión causado por las fuerzas laterales.
Nota: este apartado es un resume del siguiente artículo
Movimientos rectilíneos
La primera fuerza que entra en juego es la fuerza de tracción. La fuerza de tracción es ocasionada por la fricción del neumático contra la superficie del asfalto, que es provocada por el desplazamiento del neumático contra el asfalto debido al par motor aplicado por el motor.
El par motor es el momento de fuerza que ejerce el motor del coche sobre el eje de transmisión, expresado en N.m. El par motor que puede entregar depende de la velocidad a la cuál este gira, típicamente expresada en rpm. La relación momento torsor/rpm no es lineal, pero se representa normalmente como una curva llamada función del momento torsor (La curva exacta de cada motor viene determinada por los test que los fabricantes los someten estos motores). Aquí vemos un ejemplo para el motor del Corvette LS1(5.7 litros V8).

Curva de par motor/potencia del Corvette LS1
El eje de abscisas está expresado en revoluciones por minuto(rpm) y el de ordenadas en Caballos de potencia. La curva anterior sólo esta definida en el rango de rpm en el que trabaja el motor, que para el ejemplo es en el intervalo 1000 y 6000 rpm. La curva de par motor representa la máxima potencia que puede entregar el motor para unas rpm dadas.
El par motor se transmite a través de los engranajes hasta llegar a las ruedas, que se acaba conviertiendo en una fuerza a través del giro de estas sobre la carretera, dividido por el radio. La siguiente imagen ilustra el proceso:
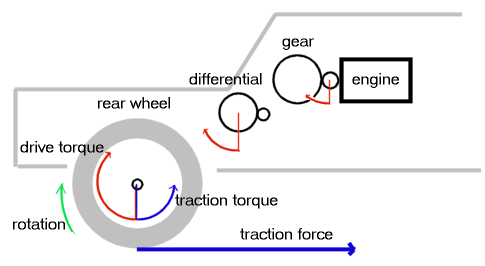
Par motor aplicado sobre el eje de tracción
A continuación podemos ver la formula que convierte el par motor proporcionado por el motor en fuerza de "conducción"; es decir, la fuerza longitudinal que ejercen las ruedas del eje de tracción sobre la carretera:
Donde:
- u es el vector unitario que refleja la orientación del coche
- Pmotor es el par motor del motor para unas rpm dadas. Expresado en en N.m
- xm es la relación de transmisión de las marchas
- xd es el coeficiente del diferencial
- n es la eficiencia de la transmisión
- Rw es el radio de la rueda.
Si esta fuera la única fuerza que influye en el movimiento, el coche aceleraría hasta alcanzar una velocidad infinita. Aquí es donde entran en juego las resistencia. A altas velocidades la mas importante es la resistencia del aire. Esta fuerza es muy importante porque es proporcional al cuadrado de la velocidad.
Donde:
- Cdrag es una constante de resistencia del aire.
- v es el vector de velocidad.
- |v| el módulo del vector.
El módulo del vector velocidad es la velocidad a la que nos referimos comunmente, expresada en km/h cuando hablamos de vehículos.
La siguiente resistencia que encontramos es la resistencia al giro. Es causada por la fricción entre la goma del neumático y la superficie de contacto debido al desplazamiento de las ruedas.
Donde:
- Crr es una constante de rozamiento.
- v el vector de velocidad.
A bajas velocidades la resistencia al giro es la mayor resistencia que encuentra el coche, mientras que a altas velocidades sería la resistencia del aire.
La fuerza logitudinal total es la suma de estas tres fuerzas:
Transferencia de peso
Un efecto importante cuando se acelera o frena es el efecto de la transferencia dinámica de peso. Cuando se frena el coche baja el morro hacia adelante. Durante la aceleración, el coche se inclina hacia atrás. Esto es debido a que el centro de gravedad el coche cambia. El efecto de esto es que el peso sobre las ruedas traseras aumenta durante la aceleración, mientras que las ruedas delanteras deben soportar menos peso. La distribución de peso afecta dramáticamente a la tracción máxima por rueda. Esto es debido a que el límite de fricción es proporcional a la carga en esa rueda:
Donde:
- mu es coeficiente de rozamiento del neumático.
Para vehiculos estacionados el peso total del coche se distribuye sobre las ruedas delanteras y traseras de acuerdo a la distancia entre el eje delantero y trasero al centro de masa:
Donde:
- b y c son la distancia al centro de gravedad de los ejes delanteros y traseros.
- L es el grosor de las ruedas.
Si el coche acelera o desacelera en un factor a, el peso frontal y trasero se calculan como sigue:
Donde:
- h es la altura del centro de gravedad,
- M es la masa del coche y
- a la aceleración

Distribución del peso del coche sobre las ruedas
Giros
Una cosa a tener en cuenta cuando estamos simulando giros es que la simulación de las propiedades física a baja velocidad es diferente de la simulación a alta velocidad. A velocidades bajas (aparcamiento, maniobras), las ruedas giran mas o menos en la dirección en la que éstas apuntan. Para simular estos giros no se necesita considerar las fuerzas y ni masas. En otras palabras, es un problema de cinética no de dinámica.
A velocidades más altas, puede ocurrir que las ruedas apunten en una dirección mientras que se muevan en otra. En otras palabras, las ruedas a veces pueden tener una velocidad que no esté alineada con la orientación de la rueda. Esto significa que hay una componente de velocidad que está en un ángulo recto a la rueda. Por supuesto, esto causa mucha fricción. Después de todo una rueda está diseñado para rodar en una dirección particular sin demasiado esfuerzo. En giros a alta velocidad, las ruedas están siendo empujadas hacia los lados y tenemos que tomar estas fuerzas en cuenta.
Vehículos en Bullet
El componente de dinámica de vehículos de Bullet ofrece una implementación basada en rayqueries, de tal manera que se lanza un rayo por cada rueda del coche. Usando como referencia el punto de contacto del rayo contra el suelo, se calcula la longitud y la fuerza de la suspensión. La fuerza de la suspensión se aplica sobre el chasis de forma que no choque contra el suelo. De hecho, el chasis del vehículo flota sobre el suelo sustentándose sobre los rayos. La fuerza de fricción se calcula por cada rueda que esté en contacto con el suelo. Esto se aplica como una fuerza hacia los lados y adelante por cada rueda; es decir, por cada rayo.
Hay una serie de clases que son importantes a la hora de utilizar vehículos en Bullet:
- btRaycastVehicle: Es la clase que modela el comportamiento del coche.
btRaycastVehicle::btRaycastVehicle( const btVehicleTuning& tuning, btRigidBody* chassis, btVehicleRaycaster* raycaster);
- btVehicleRaycaster: clase que proporciona una abstracción a la clase btRaycastVehicle para la gestión de rayqueries.
- btRigidBody: clase que representa un cuerpo rigido.
-
btVehicleTuning: clase que sirve como estructura de datos para el almacenamiento de algunos de los atributos mas importantes del vehículo. Los atributos son:
- btScalar m_suspensionStiffness: La rigidez (stiffness) de la suspensión. Se recomienda asignarle el valor de 10.0 para Todoterrenos, 50.0 para coches deportivos y 200.0 para coches de formula 1.
- btScalar m_suspensionCompression.
- btScalar m_suspensionDamping*: Coeficiente de amortiguación en el caso de que esté comprimida. Toma valores entre 0 y 1. El valor mínimo hace que la amortiguación rebote, mientras que el valor máximo sea lo mas rígida posible. Entre 0.1 y 0.3 la amortiguación se suele comportar correctamente.
- btScalar m_maxSuspensionTravelCm*: La distancia máxima que puede ser comprimida la suspensión, en centímetros.
- btScalar m_frictionSlip: El coeficiente de fricción entre el neumatico y el suelo. Para coches realistas debería tener el valor de 0.8, pero aumentando el valor mejora la conducción. Para coches de kart se aconseja asignarle un valores muy altos (10000.0).
- btScalar m_maxSuspensionForce: fuerza máxima que puede ejercer la suspensión sobre el chasis.
Para ampliar mas acerca de este tema, el autor de la implementación del módulo de vehículos escribió un documento en el que hablaba de los aspectos mas relevantes.
Veamos algo de código
A continuación vamos a explicar cómo inicializar un vehículo en Bullet, así como las operaciones mas importantes. En este ejemplo me voy a apoyar del gestor de físicas que he escrito para mi proyecto, que me abstrae a la hora de crear cuerpos rígidos, formas de colisión, etcétera. El código completo relativo al coche se puede encontrar en la clase Car de mi proyecto.
Los pasos que hay que seguir para inicializar un coche en bullet son:
- Creamos un cuerpo rígido
btVector3 car_dimensions = btVector3(1, 0.5f, 2); btBoxShape* chassis_box = physics->create_shape(car_dimensions); btVector3 origin = btVector3(0, 1, 0); btCompoundShape* compound = physics->create_compound_shape(origin, chassis_box); btQuaternion rotation = btQuaternion(btVector3(0, 1, 0), btScalar(80)); btVector3 position = btVector3(0, 0, 0); btTransform( rotation, position); int mass = 1000; Ogre::SceneNode* chassis_node = new Ogre::SceneNode("chassis_node"); btRigidBody* chassis_body_ = physics->create_rigid_body(transform, chassis_node, compound, mass); chassis_body_->setActivationState(DISABLE_DEACTIVATION);
En el fragmento anterior se crean dos formas de colisión: una caja y una forma compuesta(btCompoundShape), a la que asociamos la primera. Esto permite desplazar la caja una unidad en el eje Y, de forma que esté un poco alzada, indicandolo a través de la variable origin.
Tras esto se crea un cuerpo rígido. El primer atributo es una estructura de datos que almacena las rotaciones y la posición inicial. El segundo es un nodo de ogre, dado que mi gestor de físicas integra Bullet con Ogre. El tercer argumento es la forma compuesta que hemos creado antes y, por último, la masa del vehículo expresada en kilogramos.
El último paso consiste en indicarle a Bullet que el cuerpo rígido que acabamos de crear nunca debe ser desactivado; es decir, debe tenerlo en cuenta en todo momento en cada iteración de la simulación física. Bullet ignora algunos cuerpos rígidos que considera que no van a interaccionar en algún momento con otros cuerpos rigidos. Sin embargo, esto tiene como contrapunto que puede que el motor ignore acciones por parte del usuario, como una invocación al método de aceleración. Haciendo que nunca se desactive evitamos esto.
- Añadimos las ruedas. Para esto, usamos el método addWheel de la clase btRaycastVehicle(la clase que modela el vehículo):
btWheelInfo & btRaycastVehicle::addWheel (const btVector3 &connectionPointCS0, const btVector3 &wheelDirectionCS0, const btVector3 &wheelAxleCS, btScalar suspensionRestLength,btScalar wheelRadius, const btVehicleTuning &tuning, bool isFrontWheel);
Este método recibe:
- const btVector3 &connectionPointCS0: la posición de donde va a salir el rayo que representa la rueda. Esta posición debe estar dentro del chasis del coche o de lo contrario esa rueda no aplicará fuerza de tracción.
- const btVector3 &wheelDirectionCS0: El vector dirección de la rueda.
- const btVector3 &wheelAxleCS: El eje sobre el que estará el eje de la rueda.
- btScalar suspensionRestLength: La longitud máxima de la suspensión, en metros.
- btScalar wheelRadius: radio de la rueda,
- const btVehicleTuning &tuning: Ver explicación anterior.
- bool isFrontWheel: indica si la rueda está en el eje delantero o el trasero.
- Creamos el coche:
btDefaultVehicleRaycaster vehicle_raycaster = new btDefaultVehicleRaycaster(physics->dynamics_world_); btRaycastVehicle vehicle = new btRaycastVehicle(tuning_ , chassis_body_, vehicle_raycaster_); physics->dynamics_world_->addVehicle(vehicle);
Como vemos, el último paso consiste en crear un objeto de tipo btRaycastVehicle y añadirlo al mundo a través del método addVehicle de la clase btDiscreteDynamicsWorld. Bullet ofrece una implementación por defecto de la intefaz btVehicleRaycaster, lo que nos ahorra tener que implementarla nosotros.
Explicado el proceso de inicialización, sólo nos queda mostrar las operaciones básicas de nuestro vehículo.
Para que el coche acelere se ejecuta la siguiente función, que aplica par motor a las ruedas del coche
- void btRaycastVehicle::applyEngineForce( btScalar force, int wheel): aplica par motor a la rueda con ese índice. Los valores estan expresados en N.m.
- void btRaycastVehicle::setBrake( btScalar brake, int wheelIndex): aplica frenado a la ruedas con ese índice.
- void btRaycastVehicle::setSteeringValue (btScalar steering, int wheel): gira la rueda con ese índice los grados que indica el primer argumento.
Conclusiones
En este artículo he intentado explicar de la forma mas clara posible con qué problemas he tenido que lidiar a la hora de configurar e implementar la clase Car en mi proyecto. He dejado muchas cosas en el tintero, pero creo que lo mas importante ha quedado reflejado en este post.
Un saludo y nos vemos en el siguiente artículo.